#VAE

arxiv
documentation
csdn
深入浅出自编码器

自编码器 AutoEncoder AE

自编码器的初衷是为了数据降维，假设原始特征$x$维度过高，那么我们希望通过编码器$E$将其编码成低维特征向量$z=E(x)z=E(x)$，编码的原则是尽可能保留原始信息，因此我们再训练一个解码器$D$，希望能通过$z$重构原始信息，即$x\approx D(E(x))x\approx D(E(x))$，其优化目标一般是

引子

Variational Auto-Encoder, VAE

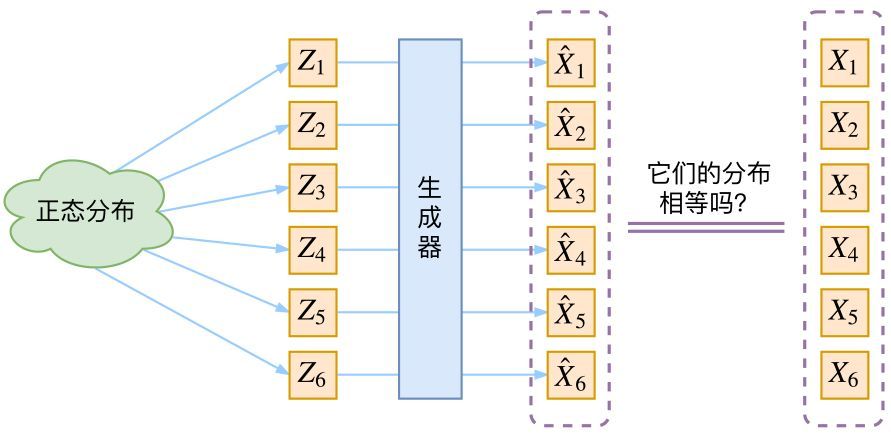
VAE与GAN类似，希望构建一个从隐变量Z生成目标数据X的模型，但是实现上有所不同。

更准确地讲，它们是假设了服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型 X=g(Z)，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式。

那现在假设服从标准的正态分布，那么我就可以从中采样得到若干个 Z1,Z2,…,Zn，然后对它做变换得到 X̂1=g(Z1),X̂2=g(Z2),…,X̂n=g(Zn)，我们怎么判断这个通过 f 构造出来的数据集，它的分布跟我们目标的数据集分布是不是一样的呢？

有读者说不是有 KL 散度吗？当然不行，因为 KL 散度是根据两个概率分布的表达式来算它们的相似度的，然而目前我们并不知道它们的概率分布的表达式。

我们只有一批从构造的分布采样而来的数据 {X̂1,X̂2,…,X̂n}，还有一批从真实的分布采样而来的数据 {X1,X2,…,Xn}（也就是我们希望生成的训练集）。我们只有样本本身，没有分布表达式，当然也就没有方法算 KL 散度。

虽然遇到困难，但还是要想办法解决的。GAN 的思路很直接粗犷：既然没有合适的度量，那我干脆把这个度量也用神经网络训练出来吧。

就这样，Wasserstien GAN 就诞生了。而 VAE 则使用了一个精致迂回的技巧。

VAE 初现

存在三个分布：

先验分布: $p(Z)$
后验分布: $p(Z|X)$